nengolib.networks.RollingWindow

class nengolib.networks.RollingWindow(theta, n_neurons, process, dimensions=6, synapse=0.1, input_synapse=0.1, dt=0.001, realizer=Balanced(), solver=LstsqL2(reg=0.001, solver=Cholesky(transpose=None), weights=False), legendre=False, **kwargs)

Approximate nonlinear functions across a rolling window of input.

Compresses the input history of finite length into a low-dimensional state to support the approximation of nonlinear functions across a rolling window of input history. This can be used to approximate FIR filters and window functions in continuous time.

Parameters:

theta : float

Width of rolling window (time-delay) in seconds.

n_neurons : integer

Total number of neurons to use in nengo.Ensemble.

process : nengo.Process

Process modelling a typical input to the network. Used to optimize the lengths of axis-aligned encoders and the distribution of eval_points. If None, then will use the defaults of uniform unit-length encoders and uniformly distributed eval_points, which usually gives sub-optimal performance.

dimensions : integer, optional

Order of PadeDelay(), or dimensionality of the state vector. Defaults to 6, which has an approximation error of less than one percent for input frequencies less than 1/theta (see pade_delay_error()).

dt : float, optional

Simulation time-step (in seconds), passed to LinearNetwork. Defaults to 0.001, but should be manually specified if the simulation time-step is ever changed.

synapse : nengo.synapses.Synapse, optional

Recurrent synapse. Bigger is typically better. Defaults to 0.1.

input_synapse : nengo.synapses.Synapse, optional

Input synapse. Typically should match the value of synapse, unless the input has already been filtered by the same synapse. Defaults to 0.1.

realizer : AbstractRealizer, optional

Method of realizing the linear system. Defaults to Balanced.

solver : nengo.solvers.Solver, optional

Solver to use for connections from the state ensemble. Defaults to nengo.solvers.LstsqL2 (with reg=1e-3).

legendre : boolean, optional

Changes the canonical realization to that of LegendreDelay(), the shifted Legendre polynomials, \(P_i(2 \theta' \theta^{-1} - 1)\). Defaults to False.

**kwargs : dictionary, optional

Additional keyword arguments passed to LinearNetwork. Those that fall under the heading of **ens_kwargs will be passed to the nengo.Ensemble that represents the state.

See also

LinearNetwork, PadeDelay(), pade_delay_error(), Balanced, EvalPoints, Encoders

Notes

This extends LinearNetwork to efficiently implement the PadeDelay() system (via Balanced, EvalPoints, and Encoders), with support for decoding nonlinear functions from the state of the network. [1]

Function are decoded from the window by evaluating the state-space at arbitrary points (as usual in Nengo), and linearly projecting them onto basis functions to express each point as a sampled window representation. See add_output() for details.

References

[1]	A. R. Voelker and C. Eliasmith, “Improving spiking dynamical networks: Accurate delays, higher-order synapses, and time cells”, Neural Computation (preprint), accepted 09 2017. [URL]

Examples

See Computing Functions Across a Rolling Window of Time for a notebook example.

>>> from nengolib.networks import RollingWindow, t_default

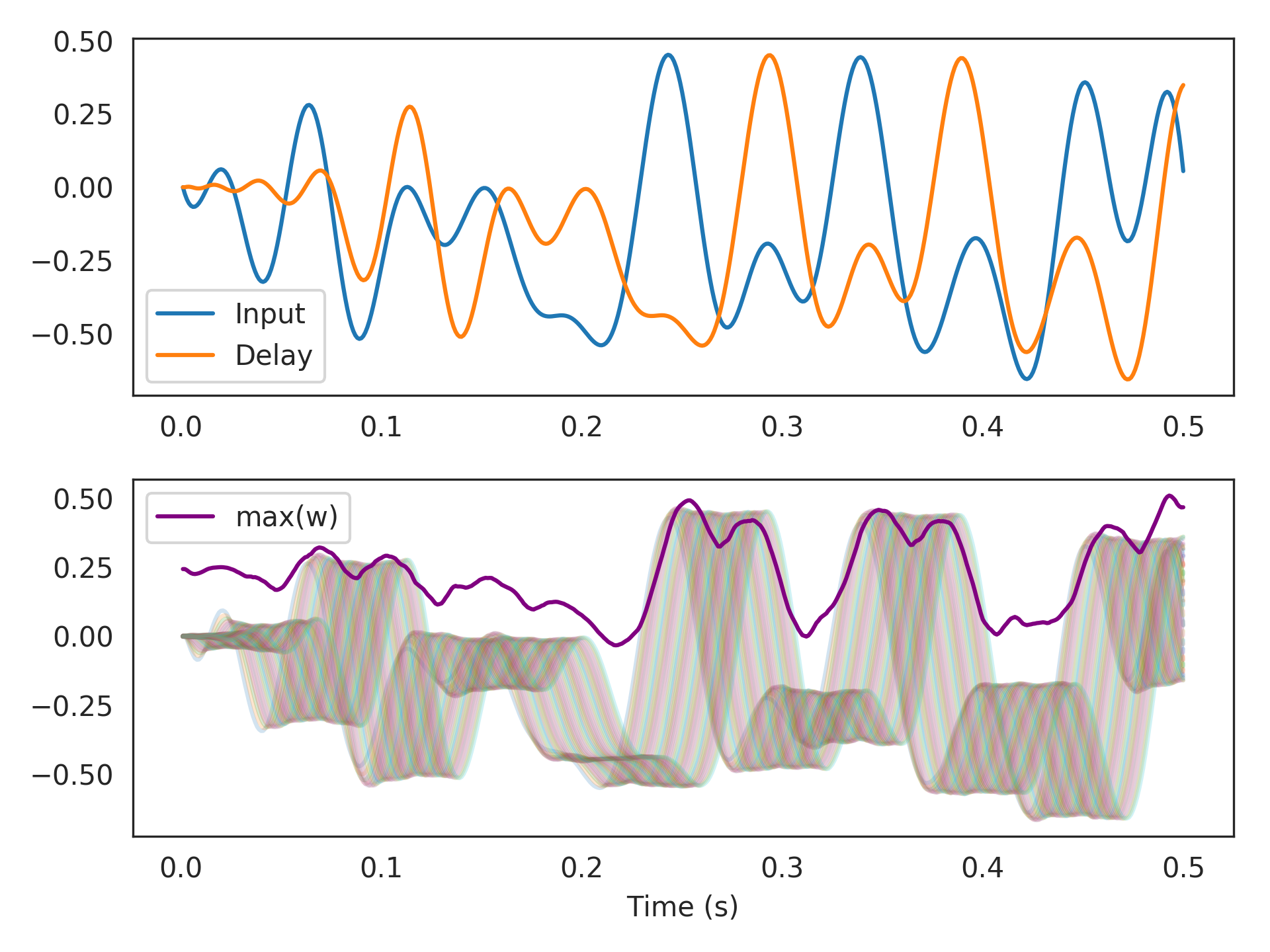
Approximate the maximum of a window of width 50 ms, as well as a sampling of the window itself. The Hankel realizer happens to be better than the default of Balanced for computing the max function.

>>> import nengo
>>> from nengolib import Network
>>> from nengolib.signal import Hankel
>>> with Network() as model:
>>>     process = nengo.processes.WhiteSignal(100., high=25, y0=0)
>>>     stim = nengo.Node(output=process)
>>>     rw = RollingWindow(theta=.05, n_neurons=2500, process=process,
>>>                        neuron_type=nengo.LIFRate(), legendre=True)
>>>     nengo.Connection(stim, rw.input, synapse=None)
>>>     p_stim = nengo.Probe(stim)
>>>     p_delay = nengo.Probe(rw.output)
>>>     p_max = nengo.Probe(rw.add_output(function=np.max))
>>>     p_window = nengo.Probe(rw.add_output(function=lambda w: w[::20]))
>>> with nengo.Simulator(model, seed=0) as sim:
>>>     sim.run(.5)

>>> import matplotlib.pyplot as plt
>>> plt.subplot(211)
>>> plt.plot(sim.trange(), sim.data[p_stim], label="Input")
>>> plt.plot(sim.trange(), sim.data[p_delay], label="Delay")
>>> plt.legend()
>>> plt.subplot(212)
>>> plt.plot(sim.trange(), sim.data[p_window], alpha=.2)
>>> plt.plot(sim.trange(), sim.data[p_max], c='purple', label="max(w)")
>>> plt.legend()
>>> plt.xlabel("Time (s)")
>>> plt.show()

(Source code)

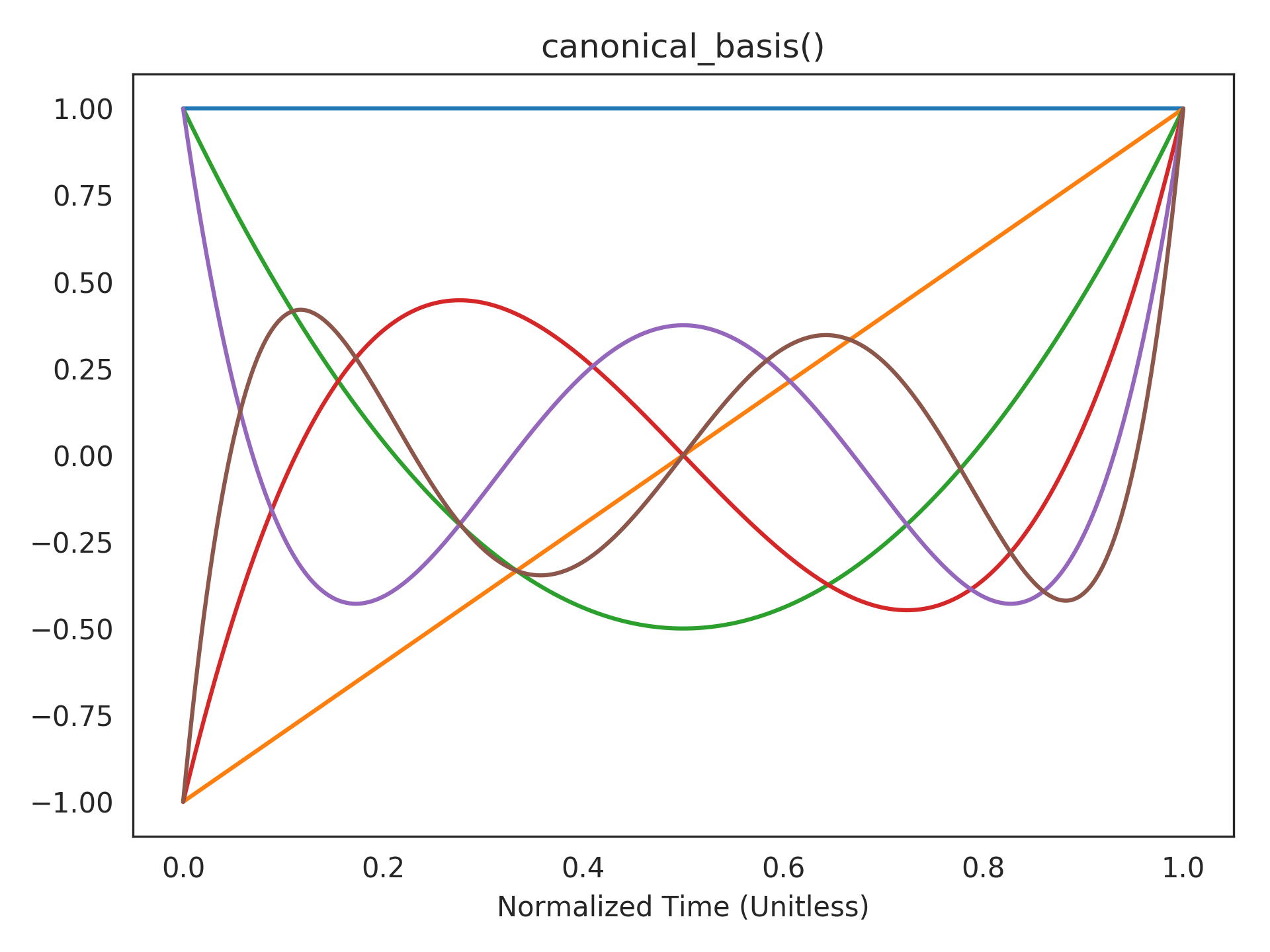
Visualizing the canonical basis functions. The state of the LegendreDelay() system takes a linear combination of these shifted Legendre polynomials to represent the current window of history:

>>> plt.title("canonical_basis()")
>>> plt.plot(t_default, rw.canonical_basis())
>>> plt.xlabel("Normalized Time (Unitless)")
>>> plt.show()

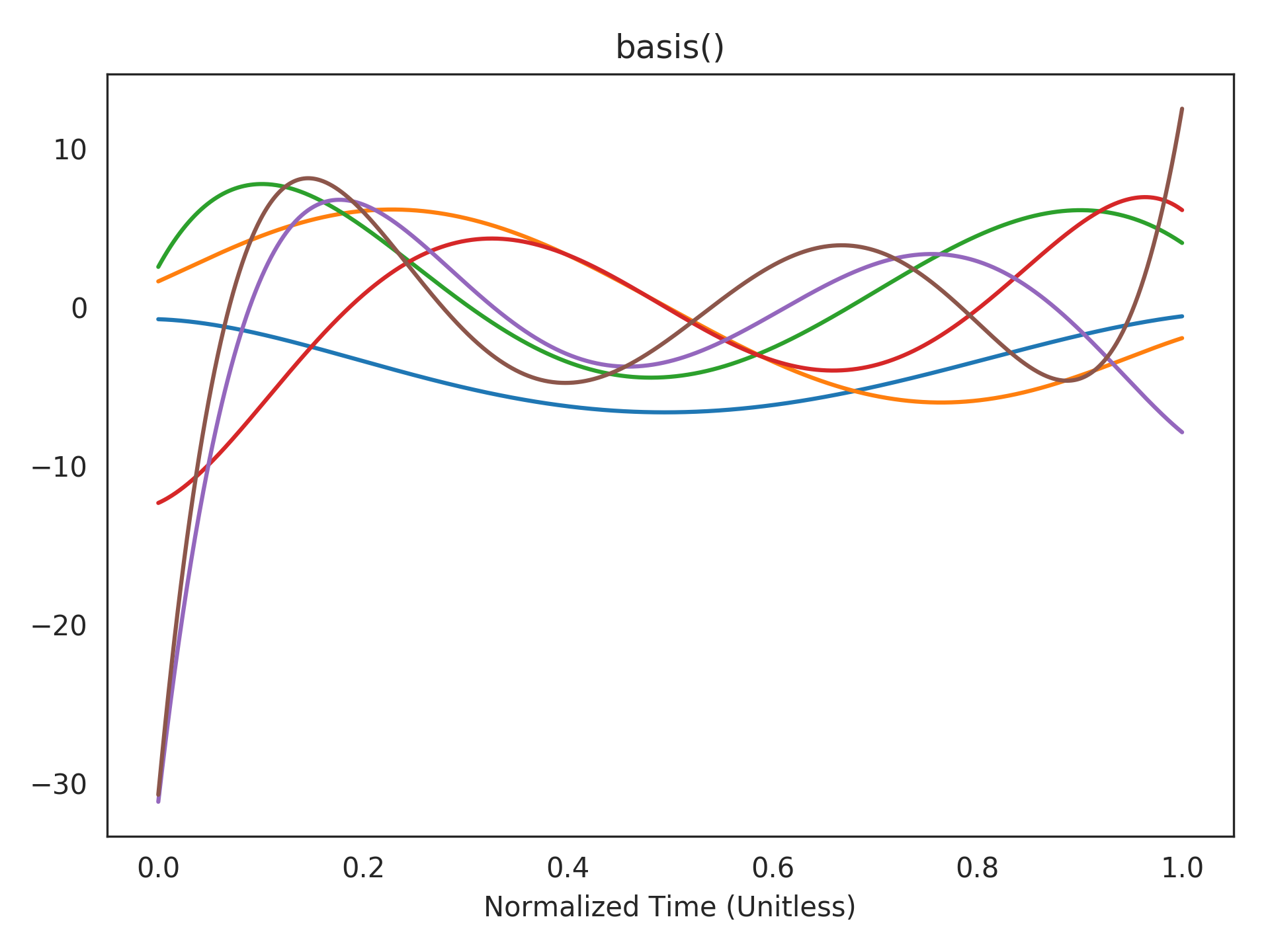
Visualizing the realized basis functions. This is a linear transformation of the above basis functions according to the realized state-space (see realizer parameter). The state of the network takes a linear combination of these to represent the current window of history:

>>> plt.title("basis()")
>>> plt.plot(t_default, rw.basis())
>>> plt.xlabel("Normalized Time (Unitless)")
>>> plt.show()

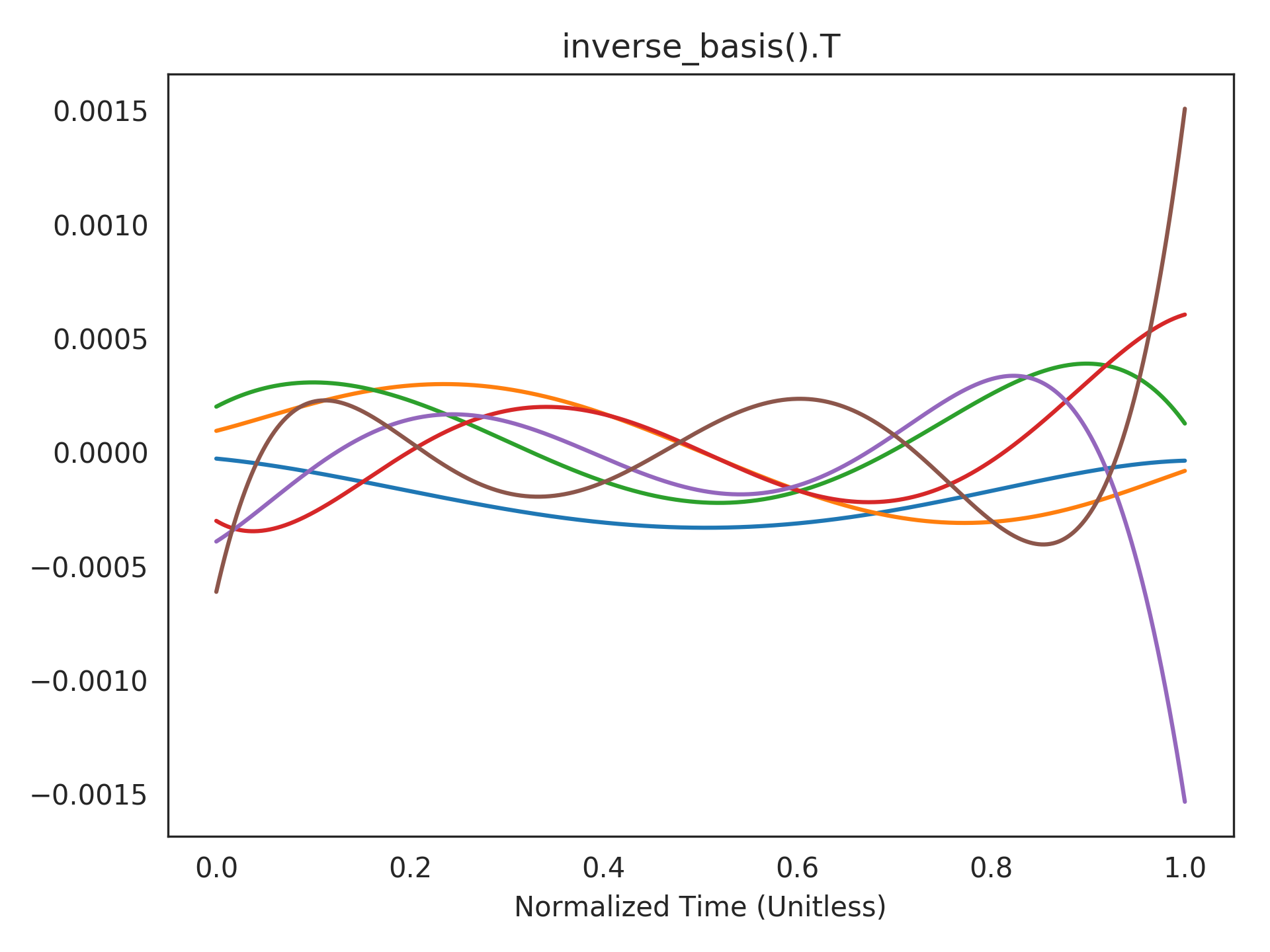
Visualizing the inverse basis functions. The functions that can be accurately decoded are expressed in terms of the dot-product of the window with these functions (see add_output() for mathematical details).

>>> plt.title("inverse_basis().T")
>>> plt.plot(t_default, rw.inverse_basis().T)
>>> plt.xlabel("Normalized Time (Unitless)")
>>> plt.show()

Attributes:

A

A state-space matrix of mapped LinearSystem.

B

B state-space matrix of mapped LinearSystem.

C

C state-space matrix of mapped LinearSystem.

D

D state-space matrix of mapped LinearSystem.

all_connections

(list) All connections in this network and its subnetworks.

all_ensembles

(list) All ensembles in this network and its subnetworks.

all_networks

(list) All networks in this network and its subnetworks.

all_nodes

(list) All nodes in this network and its subnetworks.

all_objects

(list) All objects in this network and its subnetworks.

all_probes

(list) All probes in this network and its subnetworks.

config

(.Config) Configuration for this network.

dt

A parameter where the value is a number.

input

Nengo object representing the input u(t) to the system.

input_synapse

label

A parameter where the value is a string.

mapped

Mapped LinearSystem.

n_neurons

(int) Number of neurons in this network, including subnetworks.

output

Nengo object representing the output y(t) of the system.

output_synapse

realization

Realized LinearSystem.

realizer_result

The RealizerResult produced by realizer.

seed

A parameter where the value is an integer.

size_in

Input dimensionality.

size_out

Output dimensionality.

size_state

State dimensionality.

state

Nengo object representing the state x(t) of the system.

synapse

Methods

add(obj)	Add the passed object to Network.context.
add_output([t, function, label, synapse])	Decodes a function of the window at time points -t*theta.
basis([t])	Temporal basis functions for realized PadeDelay.
canonical_basis([t])	Temporal basis functions for PadeDelay in canonical form.
default_config()	Constructs a ~.Config object for setting defaults.
inverse_basis([t])	Moore-Penrose pseudoinverse of the basis functions.

copy

add_output(t=None, function=<function RollingWindow.<lambda>>, label='output', synapse=None, **conn_kwargs)

Decodes a function of the window at time points -t*theta.

Parameters:

t : array_like, optional

A scalar or array-like with elements ranging between 0 (beginning of window) and 1 (end of window; i.e., theta). Specifies the time-points at which to sample the window’s basis functions. Defaults to the value of t_default: 1000 points spaced evenly between 0 and 1.

function : callable, optional

A function that consumes some window w of requested time-points (len(w) == len(t)), and returns the desired decoding. Defaults to returning the end of the window: w[-1].

label : string, optional

Label for the created nengo.Node. Defaults to 'output'.

synapse : nengo.synapses.Synapse, optional

Synapse passed to created nengo.Connection. Defaults to None.

**conn_kwargs : dictionary, optional

Additional keyword arguments passed to nengo.Connection.

Returns:

:class:`nengo.Node`

Node object that holds the decoded function from the state ensemble. The size of the node is equal to the output dimensionality of the provided function.

Notes

The approach is to project the state-vector onto the basis functions given by the rows of basis(), and then supply the resulting window representation to the given function. Then we solve for the decoders with respect to the state-vector as usual in Nengo.

The canonical_basis() functions are polynomials of increasing order (from 0 up to q-1, where q=dimensions). If legendre == False, then:

\[\begin{split}P_i(t) = \begin{pmatrix}q \\ i\end{pmatrix}^{-1} \sum_{j=0}^i \begin{pmatrix}q \\ j\end{pmatrix} \begin{pmatrix}2q - 1 - j \\ i - j\end{pmatrix} \left( -t \right)^{i - j} \text{,} \quad 0 \le t \le 1 \text{,} \quad i = 0 \ldots q - 1 \text{.}\end{split}\]

If legendre == True, then these are the shifted Legendre polynomials: [2]

\[\begin{split}P_i(t) = (-1)^i \sum_{j=0}^i \begin{pmatrix}i \\ j\end{pmatrix} \begin{pmatrix}i + j \\ j\end{pmatrix} \left( -t \right)^{j} \text{,} \quad 0 \le t \le 1 \text{,} \quad i = 0 \ldots q - 1 \text{.}\end{split}\]

Since the encoders are axis-aligned (when a process is given), the functions that can be accurately decoded by this approach are of the form:

\[f({\bf w}) = \sum_{i=0}^{q-1} f_i ({\bf v}_i \cdot {\bf w})\]

where \({\bf w}\) is some history, \({\bf v}_i\) are the columns of inverse_basis(), and each \(f_i\) is some unknown low-degree nonlinearity.

References

[2]	Rodrigues, Olinde. De l’attraction des sphéroïdes, Correspondence sur l’É-cole Impériale Polytechnique. Diss. Thesis for the Faculty of Science of the University of Paris) 3 (3): 361–385, 1816.