nengolib.signal.state_norm

nengolib.signal.state_norm(sys, norm='H2')

Computes the norm of each dimension of x in the state-space.

Parameters:

sys : linear_system_like

Linear system representation.

norm : string, optional

Defaults to 'H2'. Must be one of:

• 'H2' : The power of each dimension in response to white-noise input with uniform power, or equivalently in response to a delta impulse. [1]

Returns:

norms : (len(sys),) np.array

The norm of each dimension in sys.

See also

H2Norm, l1_norm()

References

[1]	http://www.maplesoft.com/support/help/maple/view.aspx?path=DynamicSystems%2FNormH2

Examples

>>> from nengolib.signal import state_norm
>>> from nengolib.synapses import PadeDelay
>>> sys = PadeDelay(.1, order=4)
>>> dt = 1e-4
>>> y = sys.X.impulse(2500, dt=dt)

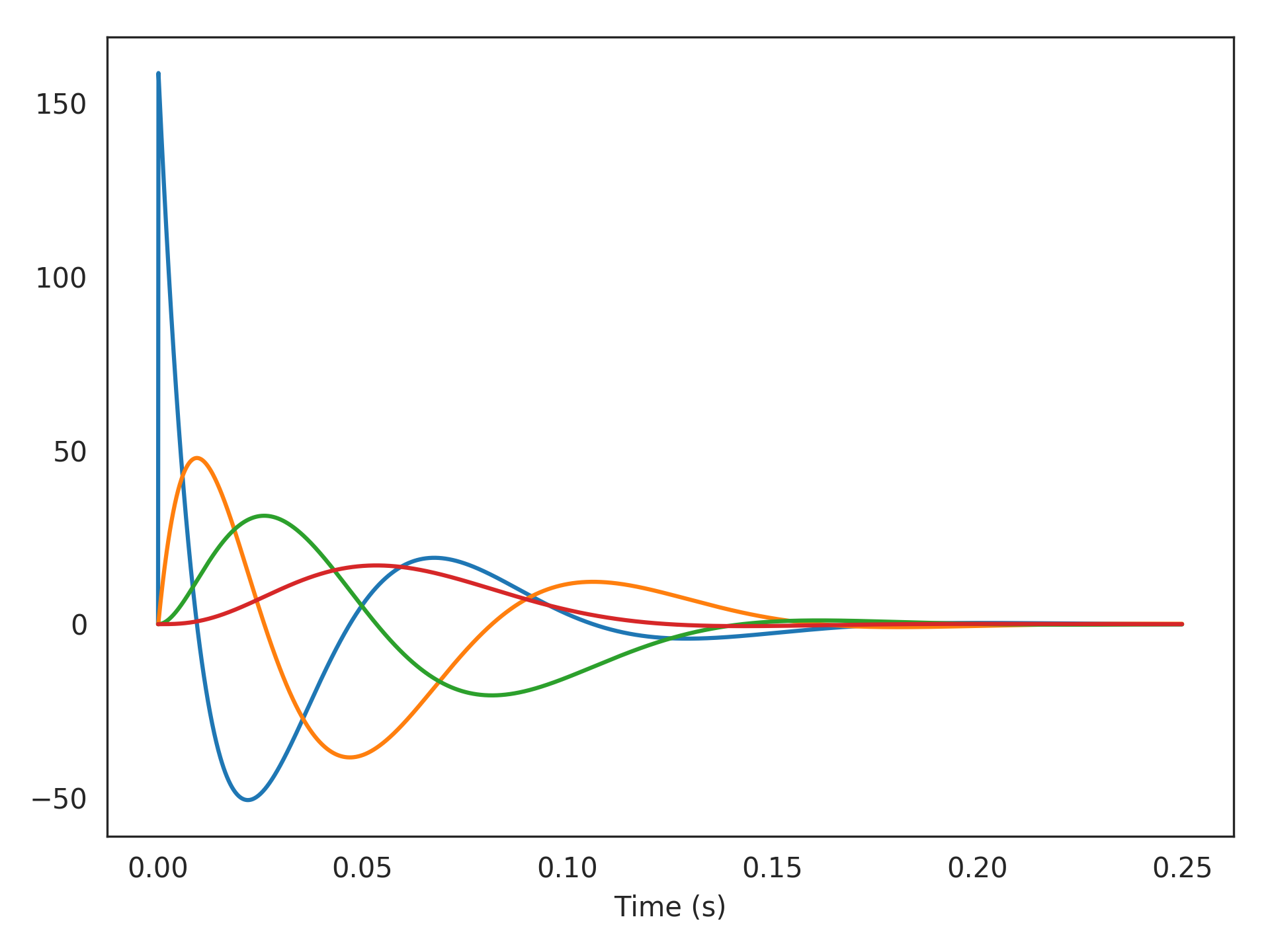
Comparing the analytical H2-norm of the delay state to its simulated value:

>>> assert np.allclose(np.linalg.norm(y, axis=0) * np.sqrt(dt),
>>>                    state_norm(sys), atol=1e-4)

>>> import matplotlib.pyplot as plt
>>> plt.plot(sys.ntrange(len(y), dt=dt), y)
>>> plt.xlabel("Time (s)")
>>> plt.show()

(Source code)