nengolib.networks.LinearNetwork

class nengolib.networks.LinearNetwork(sys, n_neurons_per_ensemble, synapse, dt, radii=1.0, input_synapse=None, output_synapse=None, realizer=Hankel(), solver=Default, label=None, seed=None, add_to_container=None, **ens_kwargs)

Network implementing a linear time-invariant (LTI) system.

This network implements the following linear state-space model:

\[\begin{split}\dot{{\bf x}}(t) &= A{\bf x}(t) + B{\bf u}(t) \\ {\bf y}(t) &= C{\bf x}(t) + D{\bf u}(t)\end{split}\]

This works by first realizing a state-space representation from the given sys and realizer, and then using ss2sim() to apply a generalization of Principle 3 from the Neural Engineering Framework (NEF) to map the system onto the given synapse. This yields a mapped system whose state-space matrices give the transformation matrices for the resulting Nengo network.

Parameters:

sys : linear_system_like

Linear system representation.

n_neurons_per_ensemble : integer

Number of neurons to use per ensemble (i.e., per dimension).

synapse : nengo.synapses.Synapse

Recurrent synapse used to implement the dynamics, passed to ss2sim().

dt : float or None

Simulation time-step (in seconds), passed to ss2sim(). If None, then this uses the continuous form of Principle 3 (i.e., assuming a continuous-time synapse with negligible time-step). If provided, then sys will be discretized and the discrete form of Principle 3 will be applied. This should always be given for digital simulations.

radii : float or array_like, optional

Radius of each dimension of the realized state-space. If a single float, then it will be applied to each dimension. If array_like, then its length must match size_state. Defaults to 1.

input_synapse : nengo.synapses.Synapse, optional

Input synapse connecting from input node. Defaults to None to discourage double filtering, but should typically match the synapse parameter.

output_synapse : nengo.synapses.Synapse, optional

Output synapse connecting to output node. Defaults to None.

realizer : AbstractRealizer, optional

Method of obtaining a state-space realization of sys. Defaults to Hankel.

solver : nengo.solvers.Solver, optional

Solver used to decode the state. Defaults to nengo.solvers.LstsqL2 (with reg=.1).

label : str, optional (Default: None)

Name of the network.

seed : int, optional (Default: None)

Random number seed that will be fed to the random number generator. Setting the seed makes the network’s build process deterministic.

add_to_container : bool, optional (Default: None)

Determines if this network will be added to the current container. If None, this network will be added to the network at the top of the Network.context stack unless the stack is empty.

**ens_kwargs : dictionary, optional

Additional keyword arguments are passed to the nengo.networks.EnsembleArray that represents the state.

See also

Network, RollingWindow, Hankel, ss2sim()

Notes

By linearity, the input_synapse and the output_synapse are interchangeable with one another. However, this will modify the state-space (according to these same filters) which may impact the quality of representation.

Examples

>>> from nengolib.networks import LinearNetwork
>>> from nengolib.synapses import Bandpass

Implementing a 5 Hz Bandpass() filter (i.e., a decaying 2D oscillator) using 1000 spiking LIF neurons:

>>> import nengo
>>> from nengolib import Network
>>> from nengolib.signal import Balanced
>>> with Network() as model:
>>>     stim = nengo.Node(output=lambda t: 100*int(t < .01))
>>>     sys = LinearNetwork(sys=Bandpass(freq=5, Q=10),
>>>                         n_neurons_per_ensemble=500,
>>>                         synapse=.1, dt=1e-3, realizer=Balanced())
>>>     nengo.Connection(stim, sys.input, synapse=None)
>>>     p = nengo.Probe(sys.state.output, synapse=.01)
>>> with nengo.Simulator(model, dt=sys.dt) as sim:
>>>     sim.run(1.)

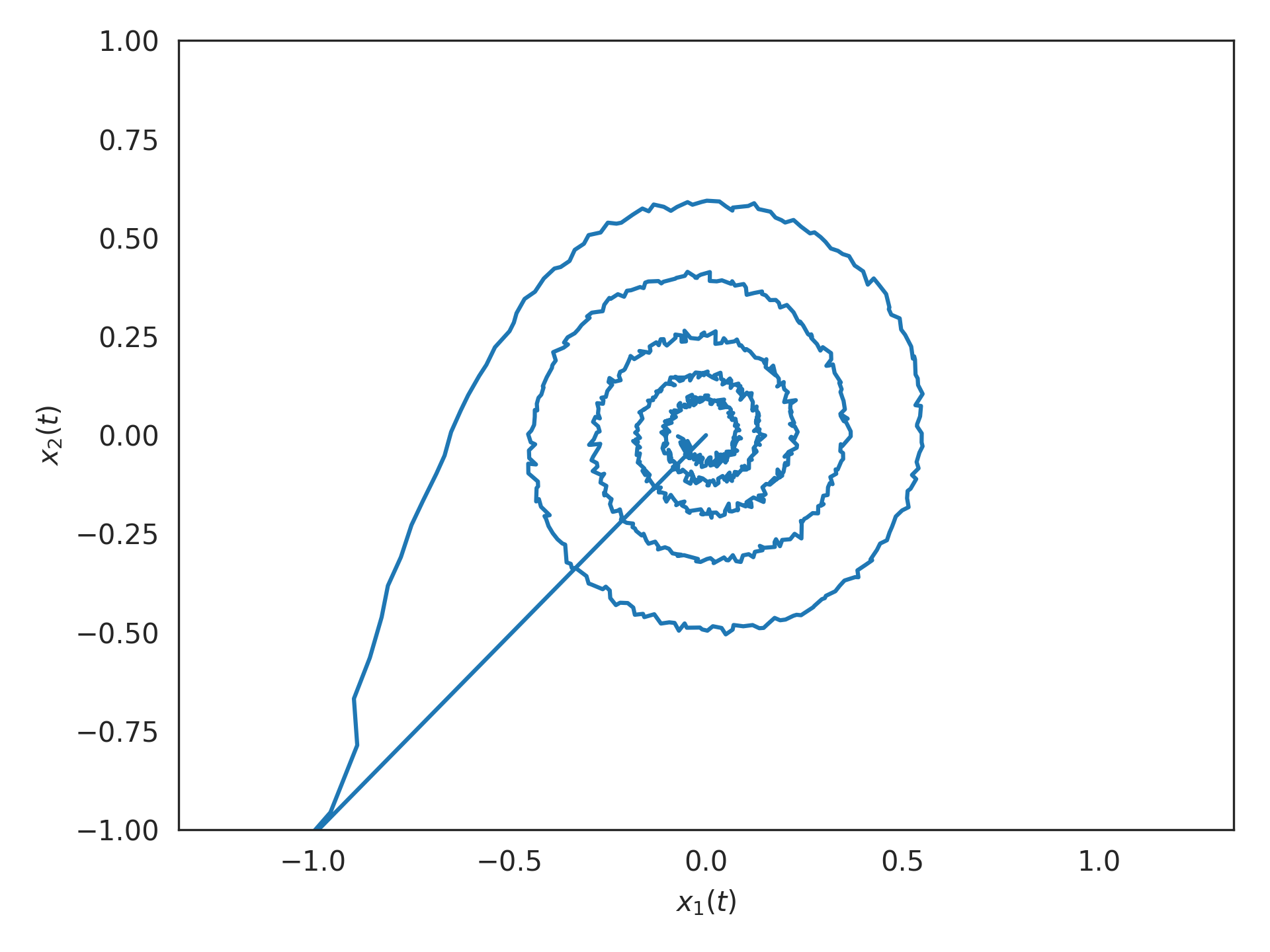
Note there are exactly 5 oscillations within 1 second, in response to a saturating impulse:

>>> import matplotlib.pyplot as plt
>>> plt.plot(*sim.data[p].T)
>>> plt.xlabel("$x_1(t)$")
>>> plt.ylabel("$x_2(t)$")
>>> plt.axis('equal')
>>> plt.xlim(-1, 1)
>>> plt.ylim(-1, 1)
>>> plt.show()

(Source code)

Attributes:

A

A state-space matrix of mapped LinearSystem.

B

B state-space matrix of mapped LinearSystem.

C

C state-space matrix of mapped LinearSystem.

D

D state-space matrix of mapped LinearSystem.

all_connections

(list) All connections in this network and its subnetworks.

all_ensembles

(list) All ensembles in this network and its subnetworks.

all_networks

(list) All networks in this network and its subnetworks.

all_nodes

(list) All nodes in this network and its subnetworks.

all_objects

(list) All objects in this network and its subnetworks.

all_probes

(list) All probes in this network and its subnetworks.

config

(.Config) Configuration for this network.

dt

A parameter where the value is a number.

input

Nengo object representing the input u(t) to the system.

input_synapse

label

A parameter where the value is a string.

mapped

Mapped LinearSystem.

n_neurons

(int) Number of neurons in this network, including subnetworks.

output

Nengo object representing the output y(t) of the system.

output_synapse

realization

Realized LinearSystem.

realizer_result

The RealizerResult produced by realizer.

seed

A parameter where the value is an integer.

size_in

Input dimensionality.

size_out

Output dimensionality.

size_state

State dimensionality.

state

Nengo object representing the state x(t) of the system.

synapse

Methods

add(obj)	Add the passed object to Network.context.
default_config()	Constructs a ~.Config object for setting defaults.

copy