nengolib.synapses.LegendreDelay

nengolib.synapses.LegendreDelay(theta, order)

PadeDelay(theta, order) realizing the shifted Legendre basis.

The transfer function is equivalent to PadeDelay(), but its canonical state-space realization represents the window of history by the shifted Legendre polnomials:

\[P_i(2 \theta' \theta^{-1} - 1)\]

where i is the zero-based index into the state-vector.

Parameters:

theta : float

Length of time-delay in seconds.

order : integer

Order of approximation in the denominator (dimensionality of resulting system).

Returns:

sys : LinearSystem

Finite-order approximation of a pure time-delay.

See also

PadeDelay(), pade_delay_error(), RollingWindow

Examples

>>> from nengolib.synapses import LegendreDelay

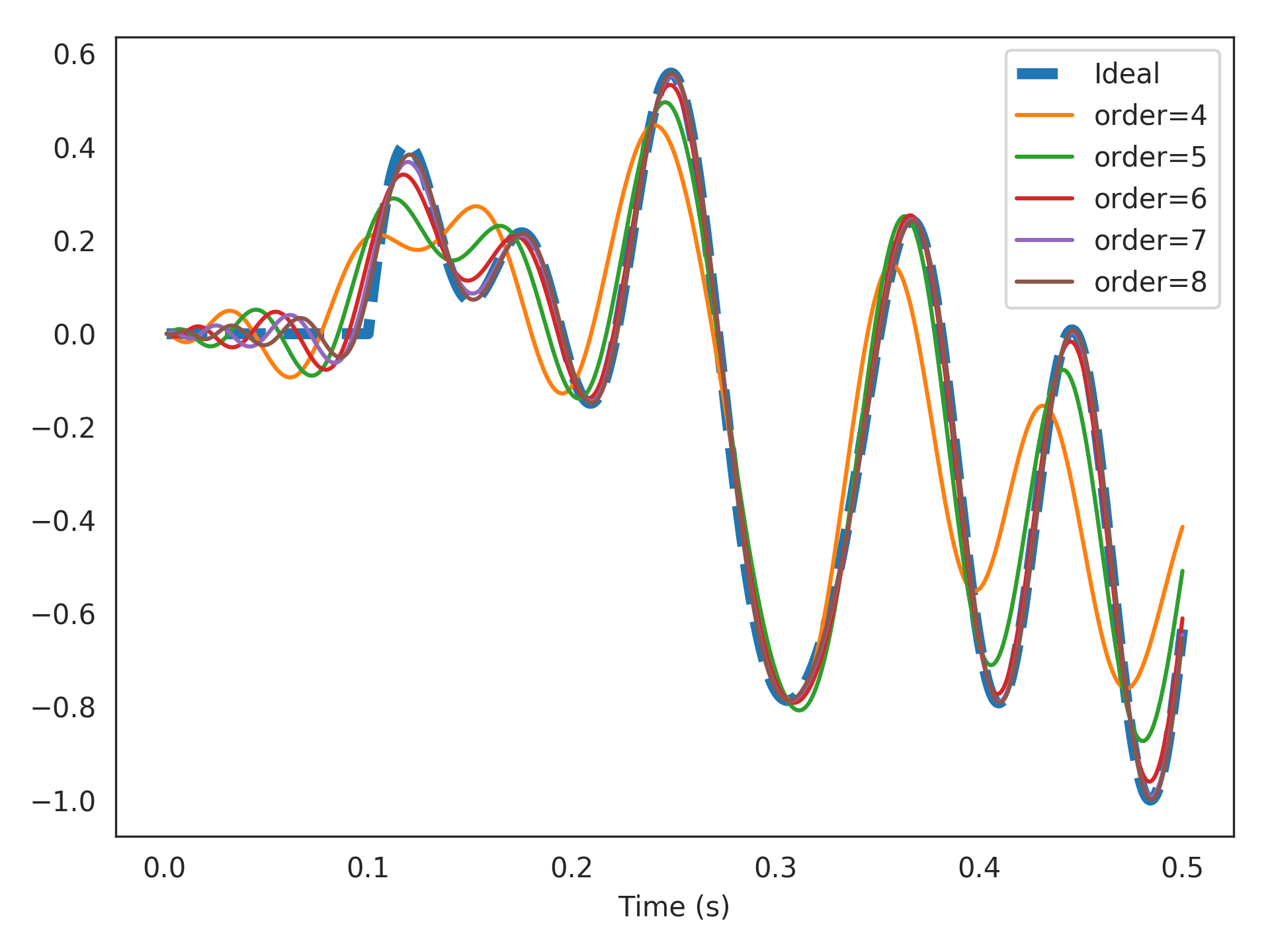
Delay 15 Hz band-limited white noise by 100 ms using various orders of approximations:

>>> from nengolib.signal import z
>>> from nengo.processes import WhiteSignal
>>> import matplotlib.pyplot as plt
>>> process = WhiteSignal(10., high=15, y0=0)
>>> u = process.run_steps(500)
>>> t = process.ntrange(len(u))
>>> plt.plot(t, (z**-100).filt(u), linestyle='--', lw=4, label="Ideal")
>>> for order in list(range(4, 9)):
>>>     sys = LegendreDelay(.1, order=order)
>>>     assert len(sys) == order
>>>     plt.plot(t, sys.filt(u), label="order=%s" % order)
>>> plt.xlabel("Time (s)")
>>> plt.legend()
>>> plt.show()

(Source code)