nengolib.stats.ScatteredHypersphere

stats.sphere = ScatteredHypersphere(surface=True, base=Rd())

stats.ball = ScatteredHypersphere(surface=False, base=Rd())

class nengolib.stats.ScatteredHypersphere(surface, base=Rd())

Number–theoretic distribution over the hypersphere and hyperball.

Applies the spherical_transform() to the number-theoretic sequence Rd to obtain uniformly scattered samples.

This distribution has the nice mathematical property that the discrepancy between the empirical distribution and \(n\) samples is \(\widetilde{\mathcal{O}}\left(\frac{1}{n}\right)\) as opposed to \(\mathcal{O}\left(\frac{1}{\sqrt{n}}\right)\) for the Monte Carlo method. [1] This means that the number of samples are effectively squared, making this useful as a means for sampling eval_points and encoders in Nengo.

See Sampling High-Dimensional Vectors for mathematical details.

Parameters:

surface : boolean

Set to True to restrict the points to the surface of the ball (i.e., the sphere, with one lower dimension). Set to False to sample from the ball. See also sphere and ball for pre-instantiated objects with these two options respectively.

Other Parameters:  

base : nengo.dists.Distribution, optional

The base distribution from which to draw quasi Monte Carlo samples. Defaults to Rd and should not be changed unless you have some alternative number-theoretic sequence over [0, 1].

See also

sphere, ball, nengo.dists.UniformHypersphere, Rd, Sobol, spherical_transform(), ScatteredCube

Notes

The Rd and Sobol distributions are deterministic. Nondeterminism comes from a random d–dimensional rotation (see random_orthogonal()).

The nengolib logo was created using this class with the Sobol sequence.

References

[1]	K.-T. Fang and Y. Wang, Number-Theoretic Methods in Statistics. Chapman & Hall, 1994.

Examples

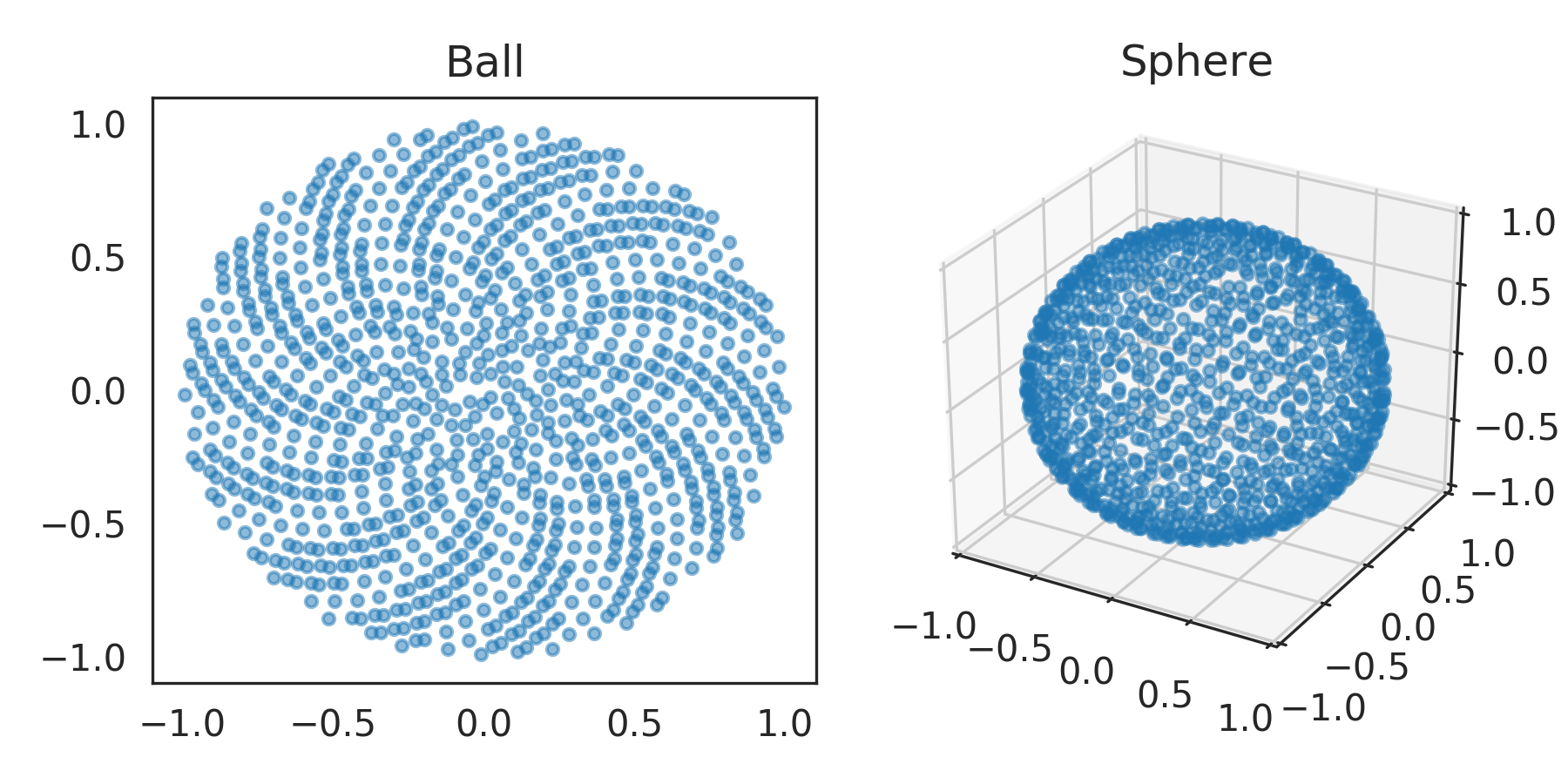
>>> from nengolib.stats import ball, sphere
>>> b = ball.sample(1000, 2)
>>> s = sphere.sample(1000, 3)

>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D
>>> plt.figure(figsize=(6, 3))
>>> plt.subplot(121)
>>> plt.title("Ball")
>>> plt.scatter(*b.T, s=10, alpha=.5)
>>> ax = plt.subplot(122, projection='3d')
>>> ax.set_title("Sphere").set_y(1.)
>>> ax.patch.set_facecolor('white')
>>> ax.set_xlim3d(-1, 1)
>>> ax.set_ylim3d(-1, 1)
>>> ax.set_zlim3d(-1, 1)
>>> ax.scatter(*s.T, s=10, alpha=.5)
>>> plt.show()

(Source code)

Attributes:

min_magnitude

A parameter where the value is a number.

surface

A parameter where the value is a boolean.

Methods

sample(n[, d, rng])

Samples n points in d dimensions.