nengolib.synapses.Highpass

nengolib.synapses.Highpass(tau, order=1)

A differentiated lowpass of given order: (tau*s/(tau*s + 1))**order.

Equivalent to differentiating the input, scaling by tau, lowpass filtering with time-constant tau, and finally repeating this order times. The lowpass filter is required to make this causal.

Parameters:

tau : float

Time-constant of the lowpass filter, and highpass gain.

order : integer, optional

Dimension of the resulting linear system. Defaults to 1.

Returns:

sys : LinearSystem

Highpass filter with time-constant tau and dimension order.

See also

Lowpass(), s

Examples

>>> from nengolib.synapses import Highpass

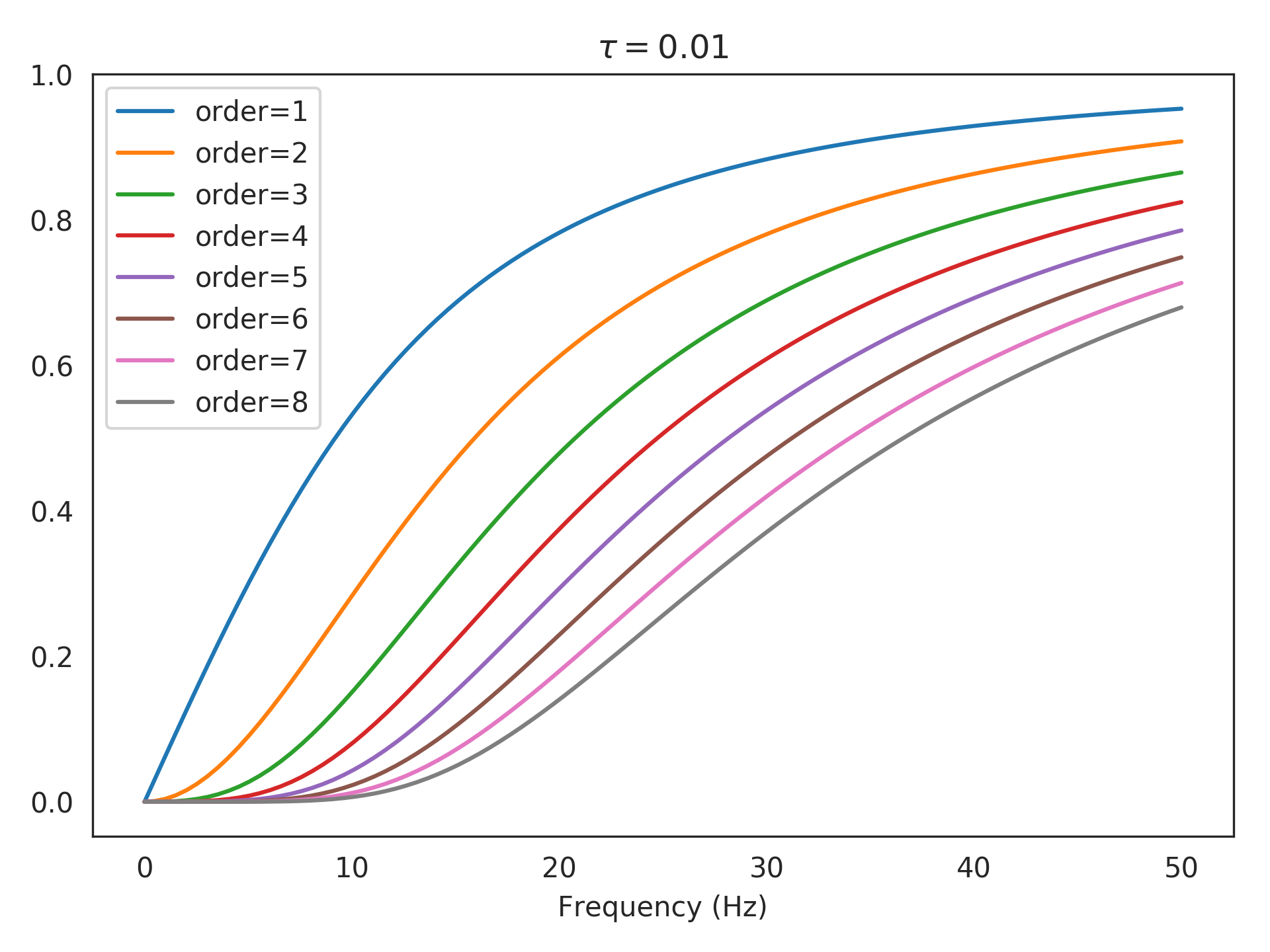
Evaluate the highpass in the frequency domain with a time-constant of 10 ms and with a variety of orders:

>>> tau = 1e-2
>>> orders = list(range(1, 9))
>>> freqs = np.linspace(0, 50, 100)  # to evaluate

>>> import matplotlib.pyplot as plt
>>> plt.title(r"$\tau=%s$" % tau)
>>> for order in orders:
>>>     sys = Highpass(tau, order)
>>>     assert len(sys) == order
>>>     plt.plot(freqs, np.abs(sys.evaluate(freqs)),
>>>              label=r"order=%s" % order)
>>> plt.xlabel("Frequency (Hz)")
>>> plt.legend()
>>> plt.show()

(Source code)